«Okay, det er vel et poeng at tittelen kan fange oppmerksomheten til leseren. Den sier likevel at matematikk i utgangspunktet er noe kjedelig som må gjøres kjekt. Er ikke matematikken i seg selv kjekk nok?»
Det er den absolutt! Matematikken er i seg selv en av de sterkeste motivasjonsfaktorene vi har. Det er ikke mye som slår følelsen av å endelig ha løst et vrient matematisk problem, gleden av å finne mønster i tilsynelatende tilfeldige system eller undringen man opplever av matematiske tryllekunstner. Matematikk er kjekt, og det har alltid vært kjekt. Matematikkundervisning er en helt annen sak.
Problemet med matematikkundervisningen
Et av de største problemene med matematikkundervisningen er at det ikke er nok problem i den[1]. Matematikkundervisning uten problem kan være med på å ødelegge elevenes naturlige nysgjerrighet, den kan frata elevene muligheten til å tenke, og den kan bidra til å redusere elevenes indre motivasjon. Elevene som ikke liker matematikk, er med andre ord et produkt av en matematikkundervisning der de ikke har fått erfare at matematikk i seg selv er kjekt.
Hvordan oppgaven presenteres
Presentasjonen av oppgaven stor betydning for hvor vellykket undervisningen blir. Det er for eksempel lettere å engasjere elevene i en oppgave dersom læreren presenterer den muntlig til elevene, enn at de bare leser oppgaven i læreboken[2]. Hvilken matematisk vinkling læreren velger under presentasjonen, har også stor betydning. Si for eksempel at elevene skal ha om areal av trekanter. Dette temaet kan presenteres på flere forskjellige måter.
Presentasjonen som et problem
Her har jeg et rektangel. I det rektangelet har jeg tegnet inn en trekant. Hvor stor er trekanten i forhold til hele rektangelet?
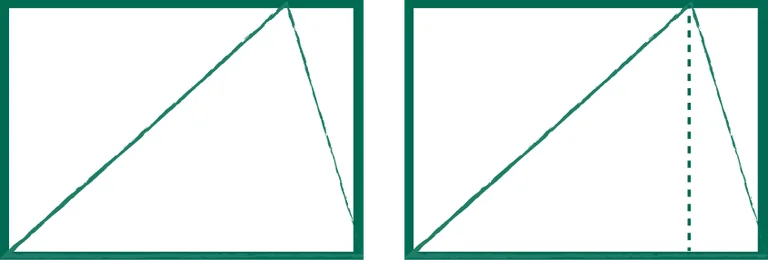
Oppgaven presenteres som et problem som elevene selv skal finne ut av. En slik presentasjon legger opp til at elevene må tenke og resonnere, de må prøve seg fram, og de må selv finne sammenhengene. Noen elever vil etter hvert finne ut at det kan være lurt å sette inn en hjelpestrek:
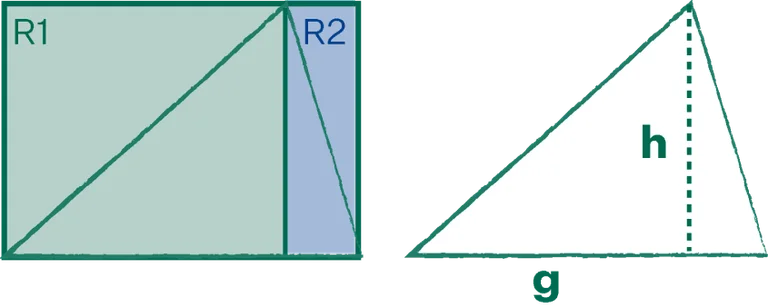
Da har vi plutselig to nye rektangler (R1 og R2), som begge er delt i to med hver sin diagonal. Trekanten består av halvparten av hvert av disse to rektanglene, og svaret på problemet trer fram: Trekanten sitt areal er halvparten av hele rektangelets areal. Dette er matematikk!
Elevene har måttet løse et problem, og i prosessen har de både kommet fram til hvordan de kan finne arealet av trekanter, og de kan begrunnet hvor formelen kommer fra. Denne tilnærmingen kan være med på å utvikle relasjonsforståelse. Elevene forstår hvorfor formelen er som den er, og de kan knytte sammenhenger til andre matematiske ideer.
Tradisjonell presentasjon
Men det er ikke slik areal av trekanter vanligvis presenteres for elevene. Ofte presenteres det som et spørsmål – og gir svaret på spørsmålet i samme slengen:
Her er en trekant med grunnlinje og høyde. For å finne arealet av trekanten bruker du denne formelen: (g x h) / 2
Det eneste som står igjen for elevene er å kopiere løsningsmetoden gitt i presentasjonen av oppgaven for å løse liknende oppgaver. Dette er ikke matematikk, men miming. En slik tilnærming kan legge opp til at elevene utvikler instrumentell forståelse, der de pugger formler og hvordan de brukes, uten å forstå hvor de kommer fra eller hvorfor de virker. Dette bidrar ikke til å utvikle tenkende elever
Vil vi at elevene skal få tenke og glede seg over matematikk, kjenne på den iboende motivasjonen for logiske oppgaver, eller skal de bare mime? Det er opp til deg, og måten du velger å presentere matematikken på.
[1] Se Paul Lockharts essay A Mathematician’s Lament for å lese mer om problemet med matematikkundervisningen. https://www.maa.org/external_archive/devlin/LockhartsLament.pdf. Eksempelet med areal av trekanter er hentet fra dette essayet.
[2] Se Peter Liljedahls bok Building Thinking Classrooms for mer informasjon om hvordan oppgaver kan presenteres.





