Del 3: Make Mathematics Fun Again

En matematisk tanke som ikke blir delt, er som et kunstverk ingen får se.

Si at vi har lyktes med å få elevene våre til å tenke matematikk. Skal elevenes tanker kun eksistere i hver elevs hode, eller skal de dele og argumentere for tankene sine?  Det viser seg at elever sannsynligvis ikke kan lære matematikk med forståelse, uten å få argumentere for tankene sine[1]. Elevenes tanker skal ikke bare eksistere i et vakum, de må få lov til å dele og diskutere dem med andre.

Kvikkbilder

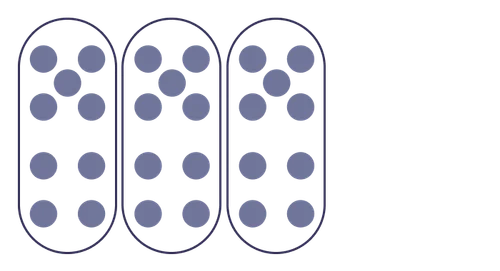
Kvikkbilder er en aktivitet som egner seg godt til å få fram matematisk diskusjon blant elevene. I denne aktiviteten får elevene kort fortalt se på et bilde med mange prikker i tre sekunder. I løpet av dette korte tidsrommet skal elevene finne ut hvor mange prikker det er på bildet. De skal også tenke over hvilken strategi de brukte. Se for deg følgende diskusjon med utgangspunkt i kvikkbildet [2]:

Lærer:  Vil noen dele en strategi?

Arild:    Jeg så det var tre femmere, altså 3x5. Så var det også tre firere, altså 3x4. Det ble 27.

Lærer:  Flott. Andre strategier?

Stine:   Jeg så at det var 5+4, som er 9. Og det var det 3 ganger. Altså 3x9=27.

Etter at flere elever har fått dele sine strategier, tar læreren ordet igjen:

Lærer:  Fint. Her ser vi at det er flere løsningsmetoder som ender opp med rett svar. Det er et viktig poeng i matematikk, at vi ikke bare er opptatt av svaret, men også hvordan vi kom fram til svaret.

Åpen strategideling og målrettet diskusjon

I eksempelet over deltar elevene i en åpen strategideling[3]. Her får de mulighet til å øve på å dele, og sette ord på hvordan de har tenkt. Det er likevel noe som mangler i diskusjonen. Læreren utfordrer ikke elevene til å sammenlikne, eller peke på matematiske sammenhenger ved de forskjellige strategiene. Dette kaller vi gjerne for en målrettet diskusjon. I eksempelet over ligger det flere muligheter for en slik målrettet diskusjon.

Prioriteringsreglene

Arild har tenkt regnestykket 3x5+3x4. Han har selv kommet fram til regnestykket, og elevene i klassen er med på at svaret er 27. Men hva skjer om de skal regne ut 3x5+3x4 skriftlig? Mange regner dette ut fra venstre til høyre:

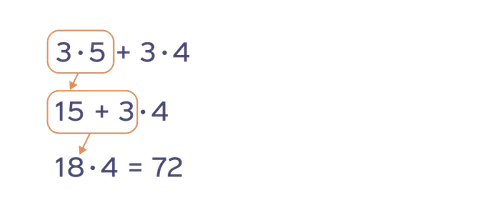
Regner ut 3x5 og får 15

Regner ut 15+3 og får 18

Regner til slutt ut 18x4 og får 72

Men det var jo ikke 72 prikker!? Dette er et eksempel på hvordan læreren kan styre diskusjonen inn på prioriteringsreglene, og elevene får selv erfare hvorfor det er et behov for dem, og at de egentlig er ganske logiske.

Parentesbruk

Stine har tenkt regnestykket (5+4)x3. Her er det for det første en fin mulighet til å komme inn på parentesbruk. Det gir mening at vi må gruppere 4 og 5 før vi multipliserer summen med 3. Da gir det kanskje også mening for elevene at vi bruker parenteser til å gruppere. For det andre kan Arild og Stine sine strategier sett i sammenheng være en fin inngang til å diskutere den distributive lov.

Nytteverdien av å diskutere

Når elevene får lov til å dele tankene sine, har dette flere positive effekter. Jeg vil særlig trekke fram tre av dem:

1. Elevene får øve på å begrunne og argumentere for løsningsstrategiene sine.
2. Læreren får mulighet til å bygge videre på elevenes tanker, og dermed lede dem inn på mer komplekse matematiske sammenhenger.
3. Når elevene setter ord på tankene sine er dette en gyllen mulighet for læreren til å kartlegge elevenes forståelse. 

Det å få elevene til å tenke matematikk er med andre ord bare halve jobben.  Vi må også få elevene til å dele og argumentere for de matematiske tankene sine. For det er få ting som er tristere enn et kunstverk ingen får se.