Målet med å bruke programmering som verktøy i klasserommet må være at det bidrar til faglig forståelse. Spørsmålet er hvordan programmering kan legge til rette for at elevene utforsker og diskuterer i de ulike fagene. Dette er utfordrende, men vi skal se på et eksempel på prosessen med å lage et undervisningsopplegg der diskusjon og utforsking er viktige elementer. Eksemplet er tatt fra Matematikk 1T, men ideene bak kan brukes i flere fag.
Programmering i Matematikk 1T
Et godt programmeringsopplegg starter med en enkel inngang (lav terskel), med mål om at alle elevene får til noe, slik at alle kan føle mestring og forhåpentligvis bli motivert.
Målet er at alle elever får til noe
Gjennom utforsking og diskusjon kan vi finne ulike måter å endre og utvide programmet på. Dette kan gjøre på flere måter og nivåer. Et eksempel er gjennom PRIMM-modellen (predict, run, investigate, modify, make) der tanken er at elevene først diskuterer hva som kommer til å skje når de kjører programmet (predict), deretter kjøre programmet (run). Deretter skal de utforske programmet (investigate) ofte gjennom å gjøre mindre endringer (modify). Til slutt kan de gjøre større endringer (modify) og lage ny kode (make) for eksempel gjennom å utvide programmet til å gjøre nye utregninger. Dette legger til rette for tilpasset undervisning.
Utforskende matematikk
I eksempelet er målet å lage et program som finner faktorene til et polynom knyttet til følgende kompetansemål i matematikk 1T:
Mål for opplæringa er at eleven skal kunne forklare polynomdivisjon og bruke det til å omskrive algebraiske uttrykk, drøfte funksjonar og løyse likningar og ulikskapar
1. Forenkle oppdraget
For at programkoden skal være enkel i starten gjør vi noen forenklinger av oppdraget. Vi antar først at alle faktorene til polynomet er heltall. Da kan vi løpe gjennom en valgt mengde heltall og sjekke om de er faktorer til polynomet. Før vi starter med å lage programmet kan spørsmål til klassediskusjonen være: «hvilke tall er det fornuftig å sjekke for, hvilket intervall?», «hvordan kan vi sjekke om et tall er en faktor til polynomet?» og «når vi finner en faktor, hvordan skal programmet gi oss denne informasjonen?»
For at elevene ikke skal sitte fast kan man gi litt hjelp i form av skjelettkode, der elevene skal fylle inn egen kode der det står spørsmålstegn (???).
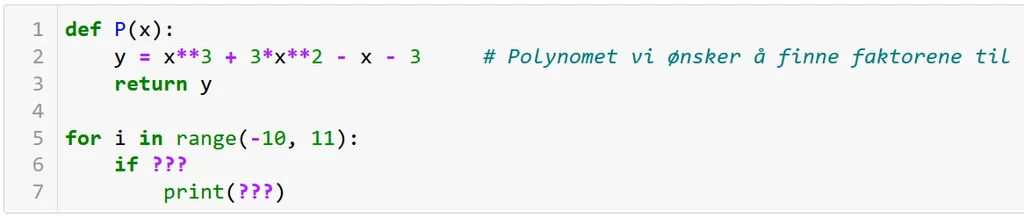
2. Kan du forbedre koden?
Mulige spørsmål i en videre diskusjonen er: «hva er svakhetene ved koden?», «er det noen polynomer koden ikke fungere for?», og «hvordan kan vi endre koden slik at den fungerer for flere/alle polynomer?». Det kan også være hensiktsmessig å diskutere fordeler med å tegne grafen til polynomet, spesielt for koblingen mellom faktoriseringen og nullpunktene.
Det er viktig å åpne opp for ulike strategier for utforsking som kan fremme matematisk forståelse.
Hvis vi for eksempel ønsker å gjøre utskriften penere kan koden endres som vist under

3. Utvider koden
Videre kan man utforske alle reelle løsninger. For eksempel, kan egenskapen være at funksjonsverdien ofte skifter fortegn ved nullpunkter? Elevene kan da diskutere hvordan man kan bruke dette til å finne alle reelle nullpunkter til en funksjon.
Hvordan finne alle reelle løsninger?
Og ikke minst, er det noen begrensninger? Et eksempel på kode (uten tegning av grafen) er:
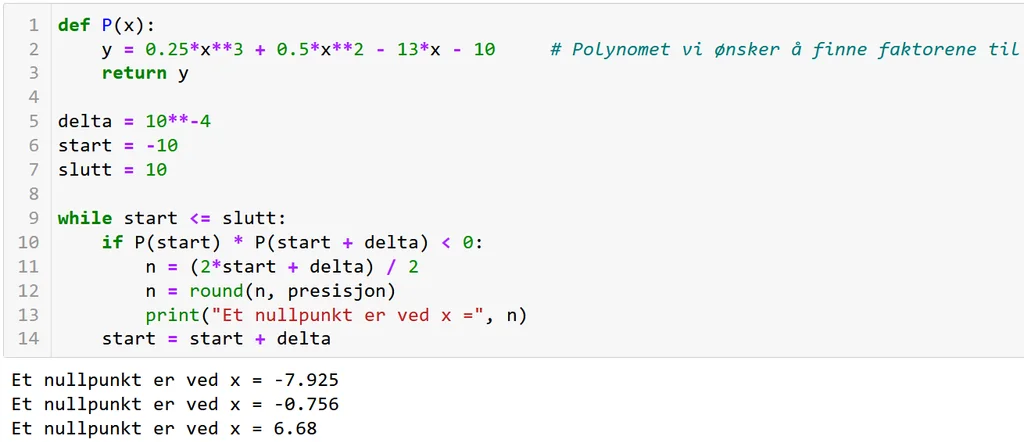
4. Diskuter med elevene
En diskusjon i etterkant kan ta opp svakheter med koden, når den ikke fungerer, og hva vi kan gjøre for å forbedre koden. Å diskutere forbedringer i koden betyr ikke alltid at elevene skal gjennomføre kodingen, det er viktigere at de beskriver endringene de ønsker å gjøre.
Hva gjør vi for eksempel med en polynomfunksjon der nullpunktet tangerer -aksen? Koden for å håndtere dette er mer komplisert, men man kan likevel diskutere hva programmet må lete etter eller sjekke for.
Diskusjonen kan dermed gå mot andre mulige strategier, for eksempel å lede elevene inn mot at en måte å sjekke for ekstremalpunkter er å se på endring av fortegnet til stigningstallet til tangenten. Her kobles flere konsepter i 1T sammen.
Kanskje flere elever vil se koblingen mellom ulike deler av pensum.
Alle elever skal få til noe i programmering
Det er selvsagt flere strategier man kan bruke, men grunnen til at jeg liker denne oppbygningen av koden og undervisningen er at den starter med en ganske enkel ide og tilsvarende enkel kode før man utvider videre. Dette gjør at koden og undervisningen har lav inngangsterskel, med gode muligheter for å utvide etter ønske og behov.
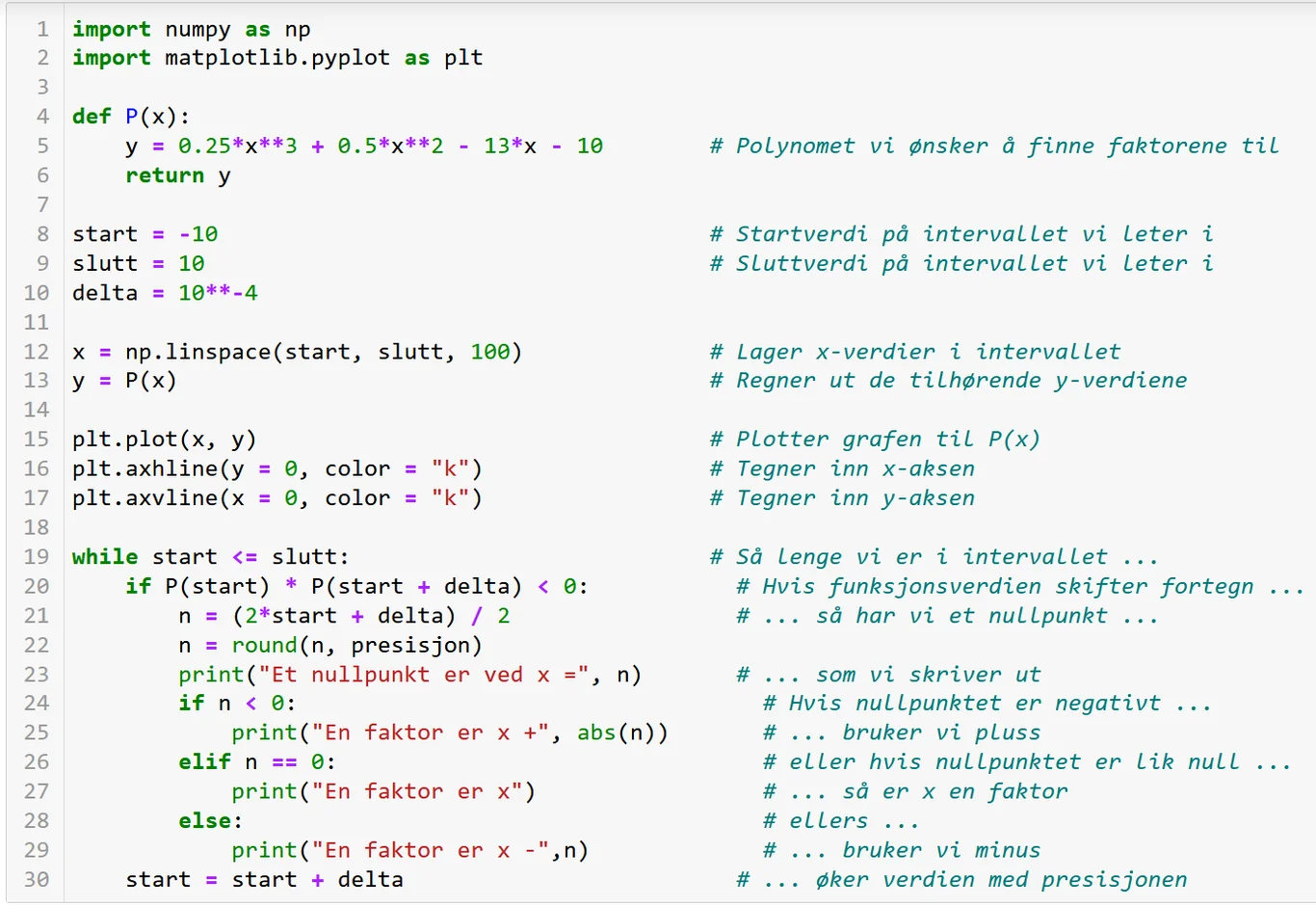
Datasettet og koden som er brukt i dette undervisningsopplegget er delt opp i to deler og fordelt utover skoleåret:






